We study LLM sparse pre-training with gradual pruning and find that the average parameter count during pre-training, rather than the final model size, predicts model quality for both sparse and dense pre-training.
Below we compare 4 pairs of sparse and dense models with matching average parameter counts.
The first shows how parameter count changes over training time for sparse vs. dense pre-training.
The second shows that sparse pre-trained models (with significantly fewer final parameters) can match the performance of their dense counterparts when they share the same average parameter count during training.
Figure 1: Different sparsity schedules for sparse pre-training of 160M parameter models with gradual pruning.
This plot compares how the parameter count changes over time for sparse vs. dense pre-training.
Figure 2: Sparse vs. dense pre-training final eval loss with matching average parameter counts.
Sparse pre-training achieves comparable performance to dense pre-training when their average parameter counts match, even though sparsely pre-training models have significantly fewer final parameters.
Unified Scaling Law with Average Parameter Count
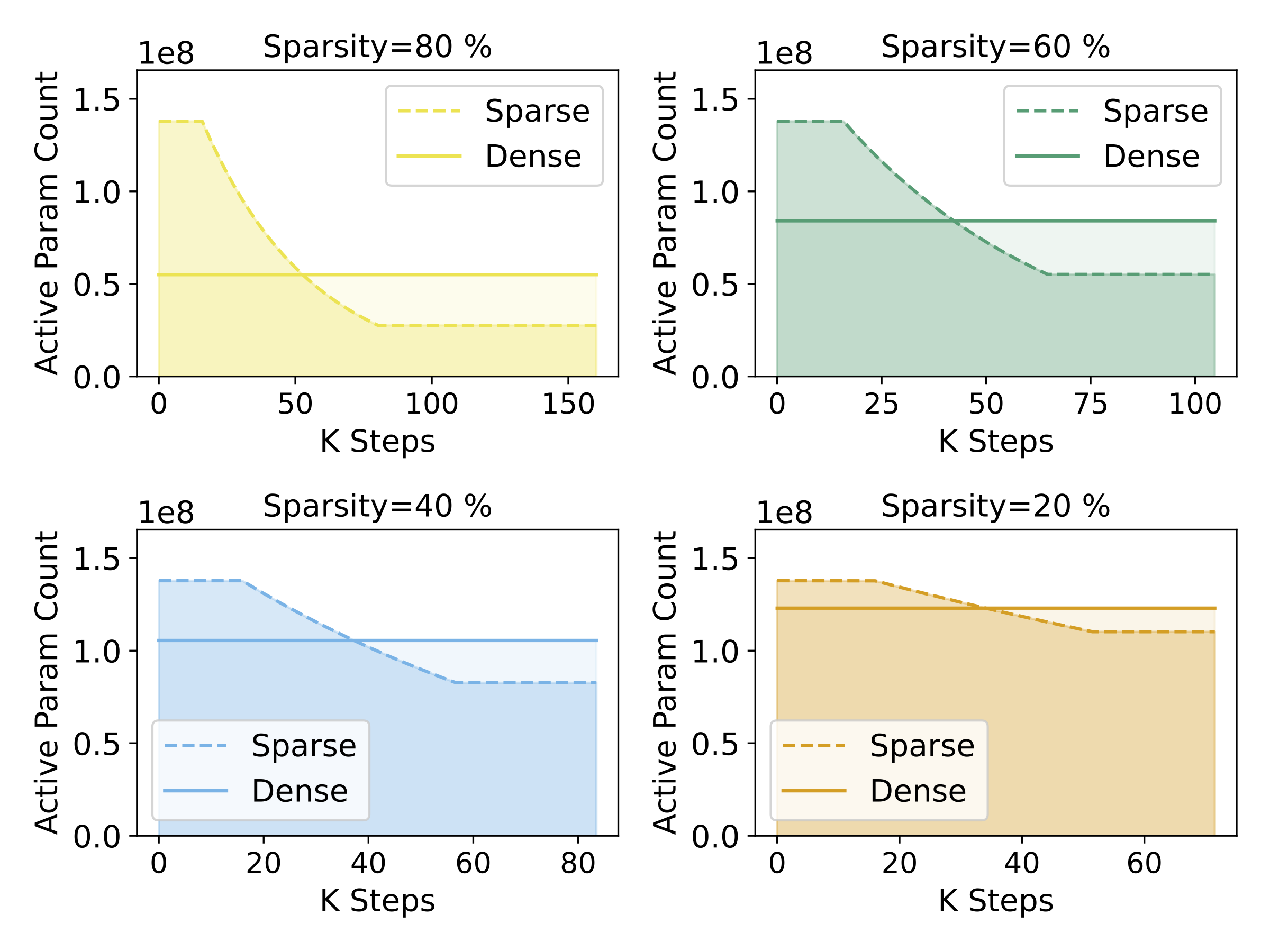
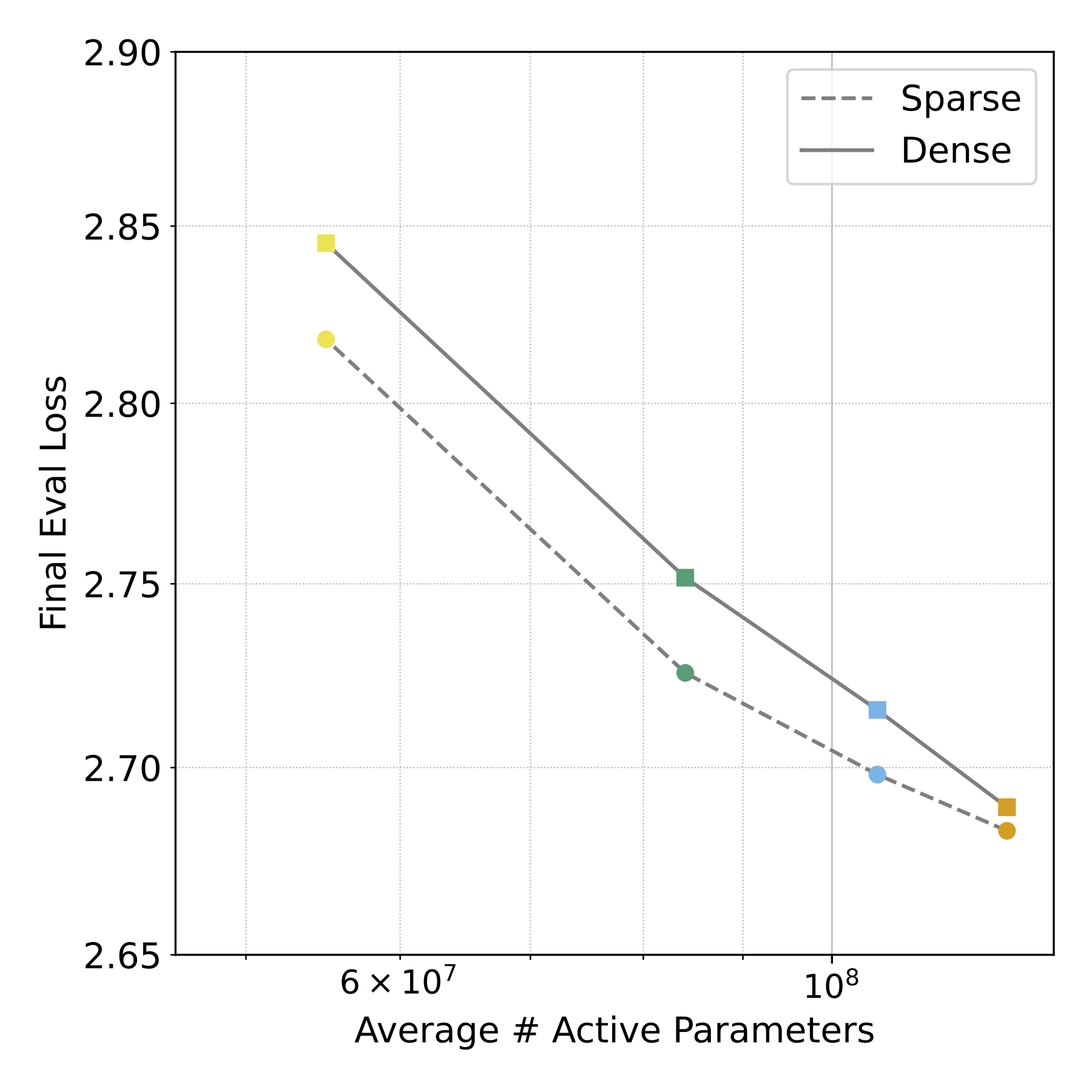
Building on this observation, we propose a modified scaling law that uses the average parameter count over pre-training as the model size term.
This approach unifies the scaling laws of both sparse and dense pre-training paradigms.
We validated this scaling law across models ranging from 58M to 468M parameters, trained with up to 20x the Chinchilla-optimal token budget.
The modified scaling law accurately predicts model performance across both sparse and dense pre-training regimes.
The original Chinchilla scaling law:
\[ L(N, D) = E + \frac{A}{N^\alpha} + \frac{B}{D^\beta} \]
Our modified scaling law using average parameter count:
\[ L(N_{\text{avg}}, D) = E + \frac{A}{N_{\text{avg}}^\alpha} + \frac{B}{D^\beta} \]
where \(N_{\text{avg}} = \frac{1}{D} \int_0^D N(t) dt\) is the average parameter count over training.
Figure 4: Our unified scaling law accurately predicts performance for both sparse and dense pre-training approaches. The plot shows the goodness of fit between predicted and actual loss values across 30 different model configurations.
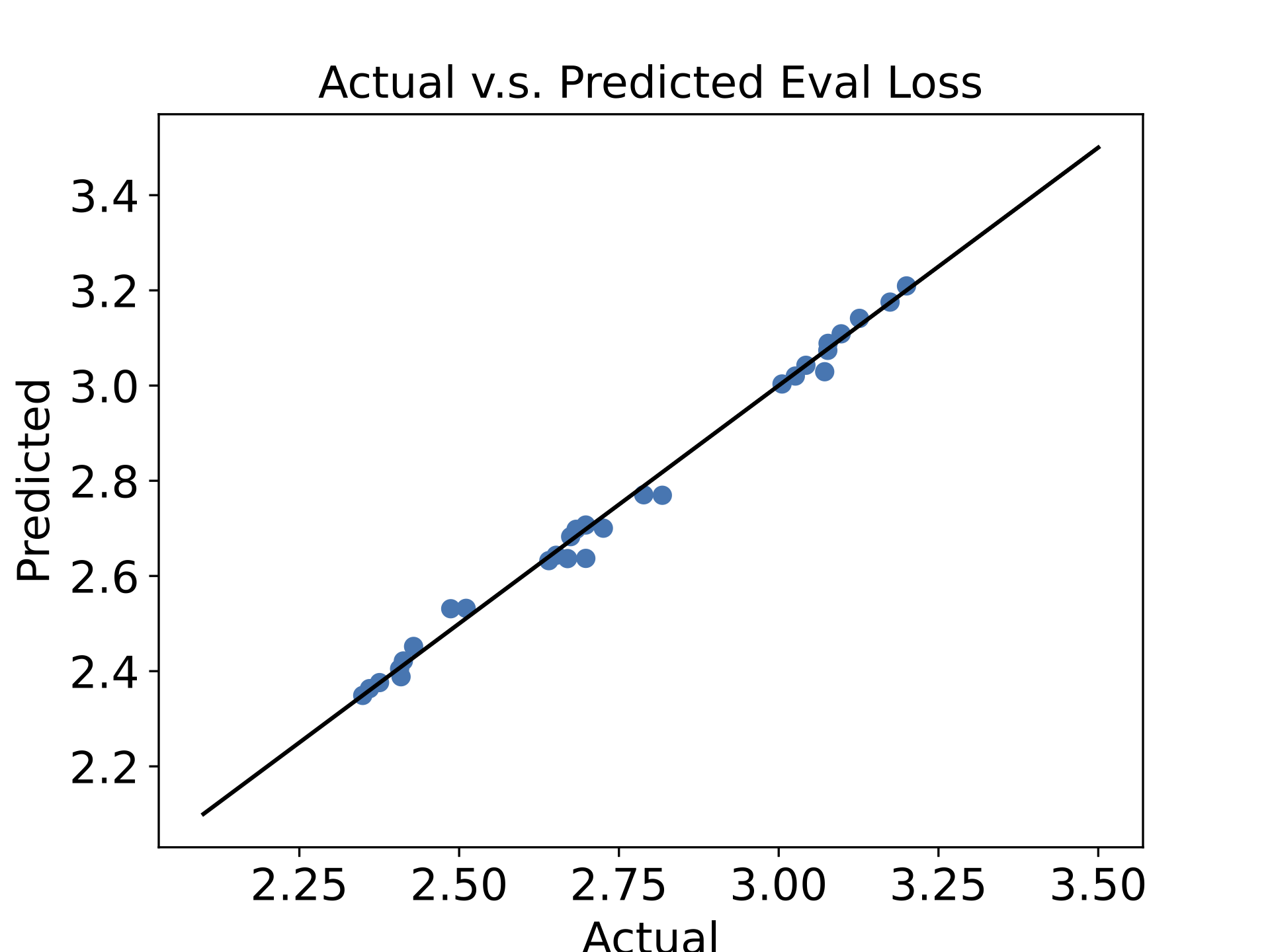
The figure above demonstrates the goodness of fit of our unified scaling law. By using average parameter count
rather than final parameter count, we can accurately predict model performance across both sparse and dense
pre-training regimes. This provides a theoretical foundation for understanding the efficiency of sparse pre-training.
The Value of Sparse Pre-training
Sparse pre-training effectively decouples average parameter count (which governs quality) from final parameter count (which determines inference costs), thus enabling a new Pareto frontier in the training cost vs. inference efficiency trade-off.
Compute v.s. Quality: Optimal sparse pre-training achieves equivalent compute versus quality trade-off as dense pre-training.
Reduced Model Size: The final models are significantly smaller, potentially requiring less compute/memory/storage.
Simplified Pipeline: Combining pruning and pre-training eliminates the need for separate pruning and fine-tuning stages.
Pre-trained Models
We're releasing 4 pairs of sparse/dense LLMs (~1B parameters) with matching average parameter counts and identical training tokens, at sparsity levels from 20-80%.
All models are hosted on Hugging Face and can be loaded using the Transformers library.
Acknowledgments
We are deeply grateful to Elias Frantar, Naveen Kumar, Sanjiv Kumar, Daniel M. Roy, and Clemens Schaefer for their valuable feedback and thoughtful review of this paper.
We also acknowledge the critical support provided by the Google CoreML Performance Team, and Google Research during this project.
We further recognize the extended team at Google DeepMind, who enabled and supported this research direction.
This work was in part supported by the Sloan Foundation, the MIT-IBM Watson AI Lab, Apple, and SRC JUMP 2.0 (CoCoSys).
Citation
@inproceedings{jin2025the,
title={The Journey Matters: Average Parameter Count over Pre-training Unifies Sparse and Dense Scaling Laws},
author={Tian Jin and Ahmed Imtiaz Humayun and Utku Evci and Suvinay Subramanian and Amir Yazdanbakhsh and Dan Alistarh and Gintare Karolina Dziugaite},
booktitle={The Thirteenth International Conference on Learning Representations},
year={2025},
}
,
Ahmed Imtiaz Humayun
